Eier über Häuser werfen

Bei mir im Kollegenkreis hat jemand behauptet, es müsse doch ganz einfach sein, ein Ei über unser Dienstgebäude zu schmeißen. Das Thema ist jetzt schon seit Wochen Gesprächsthema in unseren Kaffeerunden. Doch der mutige Kollege ist, was das Thema anbetrifft, ziemlich leise geworden. Immerhin ist das Gebäude etwa 15 m hoch und 20 m tief ... Die Wette ist auch noch nicht eingelöst. Die Wette wurde endlich am 10.06.2009 eingelöst: Das Ei ist knapp oberhalb des zweiten Stockwerkes an der Fassade des vierstöckigen Hauses zerschellt (siehe Nachtrag unten).

Natürlich haben wir gerätselt, ob es überhaupt möglich ist. Mein Ansporn war damit geweckt, mich der Beantwortung dieser Frage wissenschaftlich zu nähern. Ich wollte die Parameter derjenigen Wurfbahn berechnen, die energetisch am günstigsten ist. Hierbei gilt es, die Parameter "Abstand des Abwurfortes vom Gebäude", "Abwurfwinkel" und "Abwurfgeschwindigkeit" zu optimieren. Hierbei ist die energetisch günstigste Bahn diejenige mit der geringsten Abwurfgeschwindigkeit. Man muß schon ziemlich schnell werfen, um ein Gebäude dieser Abmessungen zu überwinden! Und die Abwurfgeschwindigkeit ist die kritische Größe, weil ein Mensch eben ein Ei nicht beliebig beschleunigen kann. Die beiden anderen geometrischen Parameter lassen sich dagegen einfacher variieren, wenngleich das Einhalten eines bestimmten Abwurfwinkels bestimmt auch nicht einfach ist.

Die Luftreibung kann bei diesem Problem nicht vernachlässigt werden, weshalb ich das Problem nicht analytisch gelöst habe, sondern die Bewegungsgleichung unter Ansatz einer Luftreibung proportional zum Quadrat der Geschwindigkeit unter Verwendung des Runge-Kutta-Verfahrens integriert habe. Diese Routine zur Integration der Bewegungsgleichung liefert dann die Wurfbahn, und eben diese Routine habe ich eingebettet in eine Monte-Carlo-Simulation . Hierbei werden die genannten Anfangsparameter in gewissen Grenzen per Zufall vorgegeben. Nach der Integration wird die resultierende Wurfbahn vom Programm daraufhin überprüft, ob sie auch tatsächlich über das Gebäude geht. Wenn ja, werden die Parameter dieser Bahn in einer Liste abgelegt. Das Spiel habe ich das Programm 100000 Mal wiederholen lassen. Danach habe ich die Liste mit den Bahnen über das Gebäude nach der Größe der Abwurfgeschwindigkeit sortieren lassen. Diejenige Bahn mit der kleinsten Abwurfgeschwindigkeit ist eine gute Näherung für die energetisch günstigste Bahn.

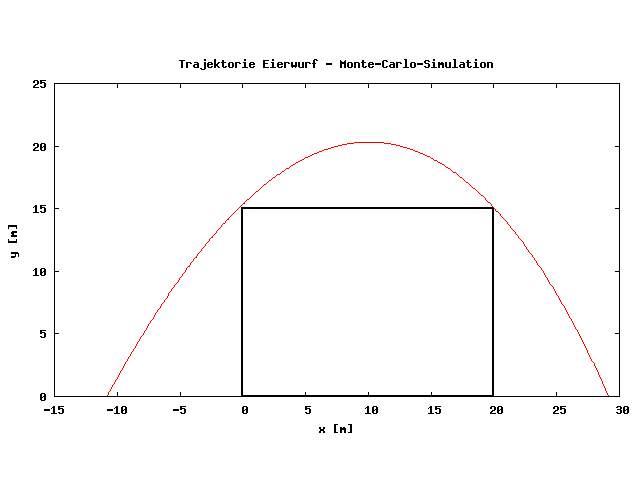
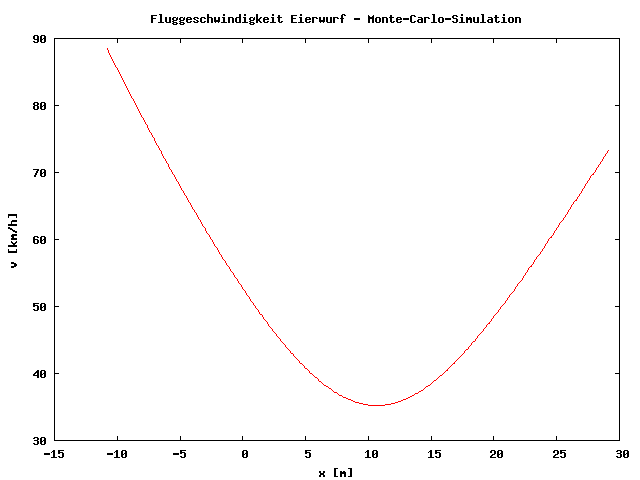
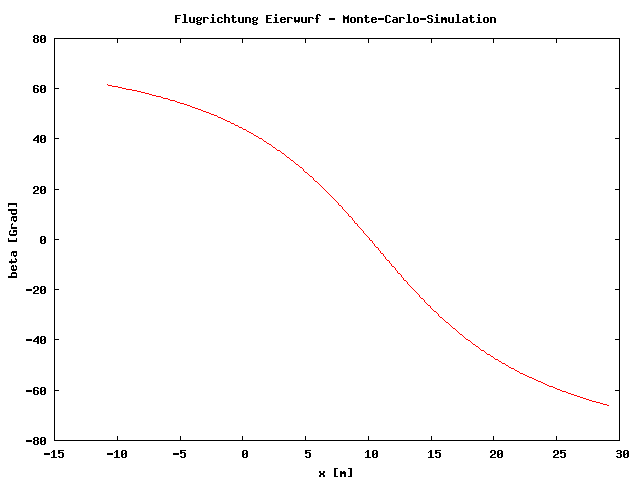
Das entsprechende Computerprogramm (Gist auf Github) habe ich in Perl geschrieben. Das Ei hat in meiner Simulation einen Durchmesser von 5 cm, ein Gewicht von 60 g und einen aerodynamischen Widerstandbeiwert von 0.3 (bezogen auf die Querschnittsfläche). Unter diesen Voraussetzungen und den weiter oben genannten Abmessungen muß sich der Werfer etwa 11 m vor das Gebäude stellen und das Ei im 60°-Winkel mit einer Geschwindigkeit von knapp 90 km/h abwerfen. Dann geht das Ei knapp über beide Dachkanten. Im Fuß- oder Handball werden Spitzengeschwindigkeiten von 100 bis 140 km/h erreicht. Also, einfach sollte es nicht sein, aber immerhin möglich.

Meine Simulation ist natürlich nur eine Idealisierung des tatsächlichen Problems. Entscheindende Faktoren habe ich außer Acht gelassen. So hat sicherlich der Wind einen enormen Einfluß auf die Flugbahn des Eis. Außerdem wird die Flugbahn drastisch beeinflußt, wenn das Ei während des Fluges rotiert. Sowas nutzen bspw. Fußballer aus ( Bananenflanke , Magnus-Effekt ). Aber diese Effekte zu berücksichtigen bedeutete eine erhebliche Steiegrung der Komplexität der Simulation - dafür habe ich dann doch keine Zeit. Aber interessant wär's schon ...

Nachtrag 15.06.2009

Am 10.06.2009 war es dann soweit: Der Kollege hat das Ei tatsächlich geworfen! Leider war ich nicht dabei, aber er hat es wohl bis knapp über das zweite Stockwerk geschafft. Leider hat das Gebäude aber vier Stockwerke, also Wette nicht gewonnen! Da das Ei gekocht war, hat es an der Wand auch keinen große Sauerei hinterlassen.