Newcomb-Benford-Analyse Bundestagswahl 2005

Der polnischer Astrophysiker Boudewijn F. Roukema hat die offiziellen Ergebnisse der Präsidentschaftswahlen im Irak vom 12. Juni 2009 einer statistischen Analyse unterzogen. Seine Ergebnisse liefern Hinweise darauf, daß die Wahlergebnisse manipuliert sein könnten. Er untersuchte die Häufigkeit der Anfangsziffern in den Stimmzahlen der Wahlkreise, die in empirischen Datensätzen häufig der sog. Newcomb-Benford-Verteilung folgt. Die gleiche Methode habe ich auf die Ergebnisse der Bundestagswahl 2005 angewendet. Leider führt hier die Methode zu keinem auswertbaren Ergebnis, da die Voraussetzungen an das Zahlenmaterial in diesem Fall nicht erfüllt werden.

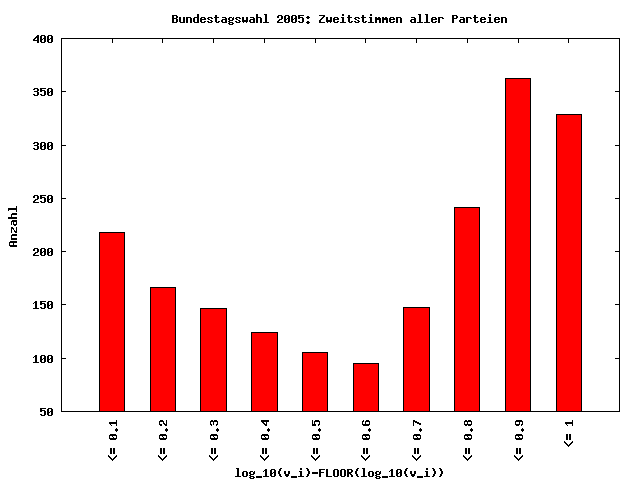
Das Newcomb-Benfordsche Gesetz (NBG) macht eine Aussage darüber, wie häufig in einem Datensatz Zahlen mit bestimmten Anfangsziffern vorkommen. Hierbei ist es so, daß Zahlen mit niedrigen Anfangsziffern häufiger vorkommen als solche mit hohen Anfangsziffern. Konkret sollten demnach etwa 30% der Zahlen mit einer 1, etwa 18% mit einer 2 und lediglich etwa 5% mit der Ziffer 9 beginnen. Hierbei muß jedoch der Datensatz gewissen Anforderungen entsprechen: Er sollte hinreichend viele Zahlen enthalten, um eine vernünftige Statistik machen zu können, die Zahlen des Datensatzes sollten einige Größenordnungen umspannen und der Datensatz sollte log-normalverteilt sein. Letzteres bedeutet, daß wenn man den dekadischen Logarithmus aller Zahlen bildet, denn Ganzzahl-Anteil der Logarithmen ignoriert (betrachte also nur die Mantisse der Logarithmen), die so gewonnenen Werte gleichverteilt sein sollten. Das NBG gilt für eine Vielzahl von Datensätzen, insbesondere jedoch für solche, denen natürliche Wachstumsprozesse zugrundeliegen.

Wie Roukema zeigt, sind die oben beschriebenen Bedingungen für die von ihm verwendeten Ergebnisse der Wahl im Iran erfüllt. Seine Analysen zeigen, daß bei der Anzahl der Wahlstimmen in den Wahlkreisen für den Kandidaten Mehdi Karrubi signifikant viele mit der Ziffer 7 beginnen, mehr als man es nach dem NKG erwarten würde. Weiterhin führt Roukema aus, daß Abweichungen der Wählerstimmen für den Amtsinhaber und Wahlsieger Ahmadinedschad daher stammen könnten, daß einzelne Stimmzahlen durch Hinzufügen von Ziffern vergrößert wurden. Weiterhin hat er sich die Verteilung der abgegebenen Stimmen für einen Kandidaten angeschaut und festgestellt, daß diese unterschiedlich gestaucht bzw. gestreckt sind. Hieraus kann man ablesen, wie stark unterschiedlich in den Wahlkreisen für einen Kandidaten gestimmt wurde. Roukemas tolle Arbeit kann man hier als PDF herunterladen .

Leider läßt sich das NBG so einfach nicht auf die Ergebnisse der Bundestagswahl 2005 anwenden. Zunächst einmal unterscheiden sich die Bundestagswahl 2005 und die Präsidentschaftswahl im Iran sehr. Im Iran wurden in jedem Wahlkreis die gleichen vier Kandidaten gewählt. Bei der Bundestagswahl treten in jedem Wahlkreis unterschiedliche Direktkandidaten an (Erststimme), und manch eine Partei ist nicht in jedem Wahlkreis wählbar (Zweitstimme). Daher verwende ich zunächst für die Analyse einen Subset der Daten. Herausgepickt habe ich mir die Zweitstimmen aller Wahlkreise für die SPD.

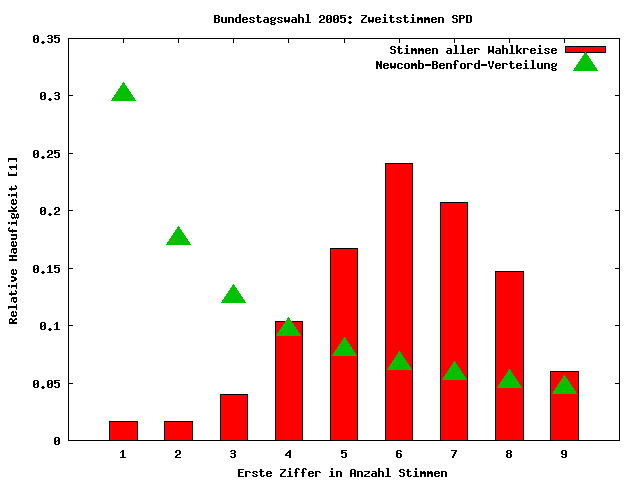
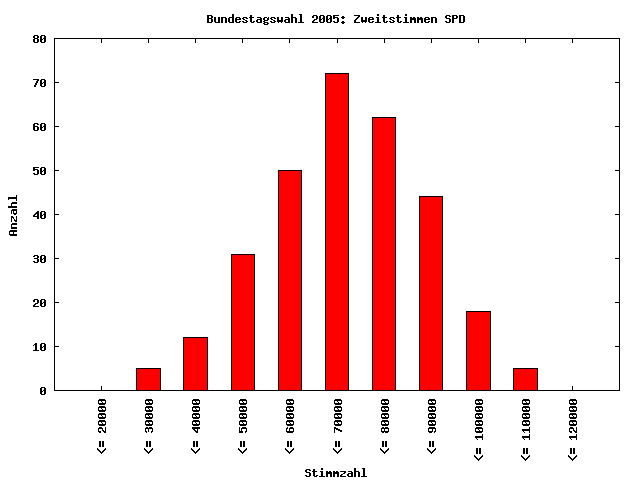
Wie man sieht, weicht die Verteilung (rote Balken) deutlich von der Verteilung nach dem NBV (grüne Dreiecke) ab. Der Grund hierfür ist, daß die zugrundeliegenden Daten nicht hinreichend weit verteilt sind. Das hat folgende Gründe: Zum einen sind die Wahlkreise in Deutschland ähnlich groß. Da jeder Wahlkreis einen Direktkandidaten in den Bundestag entsendet, muß das auch so sein, da sonst Stimmen eines kleinen Wahlkreises mehr "wert" wären als die eines großen. Zum anderen ist die Wahlbeteiligung und das Wählerverhalten in den Wahlkreisen nicht sonderlich unterschiedlich. Dies hat zur Folge, daß aus allen Wahlkreisen ähnlich viele Stimmen für die Parteien resultieren. Eine solch spezielle Verteilung der Daten führt jedoch dazu, daß diese eben nicht log-normalverteilt sind. Wendet man nun eine NBG-Analyse an, ist das Ergebnis nicht interpretierbar.





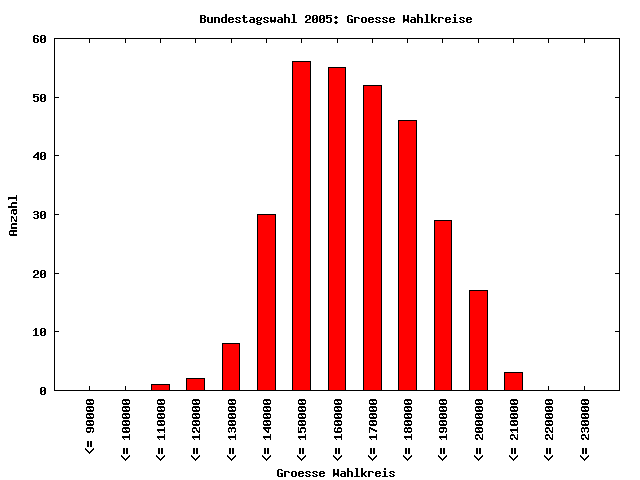
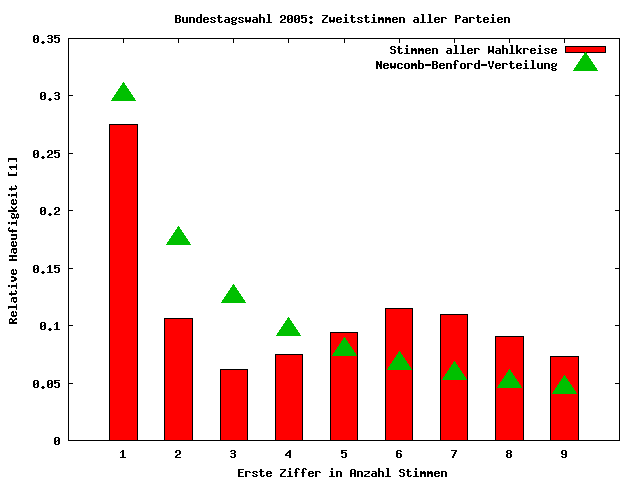
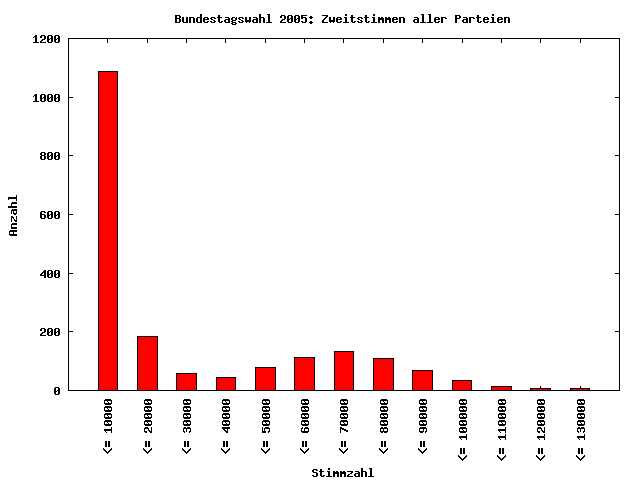
Nun habe ich die Analyse auf alle Zweitstimmen ungleich Null für alle Parteien aus allen Wahlkreisen ausgeweitet. Nun beinhaltet der Datensatz Zahlen im einstelligen Bereich bis hin zu Stimmzahlen weit über 100000. Überraschenderweise ist auch dieser Datensatz nicht ausreichend gut log-normalverteilt, um hier eine sinnvolle NBG-Analyse durchführen zu können, was mich dann doch schon überrascht hat. Allerdings liegt hier die Verteilung der Anfangsziffern schon deutlich näher an der Verteilung nach dem NBG. So ist deutlich zu erkennen, daß die Ziffer 1 klar am häufigsten auftritt. Bei den Ziffern 6 und 7 prägt sich ein kleiner "Buckel" durch, der vermutlich durch die Wählerstimmen für die großen Parteien SPD und CDU generiert wird.

Das Programm, mit welchem ich die Untersuchung gemacht habe, kann hier als Archiv heruntergeladen werden.